Uno de los recursos más atractivos que ofrece el HTML es que permite incluir elementos gráficos y sonoros que enriquecen la información. Ahora bien, tanto unos como otros suelen emplear bastante tiempo en descargarse completamente, por lo que habrá que manejarlos con prudencia y recurrir a las técnicas necesarias para minimizar su tamaño.  

A lo largo de las páginas precedentes han ido apareciendo referencias a la inclusión de imágenes en las páginas HTML. De hecho podemos dar por sabido el procedimiento básico para insertar una imagen. Veremos pues el tipo de imágenes que podemos utilizar y algún truquillo para acelerar la carga de las páginas. 

La división en bloques se ha realizado para facilitar la navegación y distribuir los contenidos en segmentos relacionados:

• Conceptos generales sobre la imagen
• Formatos gráficos para la WEB
• Escalar imágenes
• Recortar imágenes y crear rótulos
• Insertar imágenes con Composer
• Líneas. El truco de la imagen fantasma

¿Cómo se construye la imagen en la pantalla del ordenador?

Tipos de imagen

A grandes rasgos podríamos dividir las imágenes digitales en dos grandes grupos:

• Imágenes vectoriales, en las que la información de cada uno de los puntos se recoge en forma de ecuación matemática que lo relaciona con el resto de los puntos que forman la imagen. Ofrecen la gran ventaja de que la calidad de la imagen no varía al modificar el tamaño, ya que la información de cada punto no es absoluta sino relativa al resto de la imagen. Además, debido a su definición matemática apenas ocupa espacio, ya que una fórmula que represente su forma es suficiente para representar todos los puntos que la componen. Es el tipo adecuado para el diseño de línea y figura. El formato actualmente sugerido por el W3C es el denominado SVG pero su implementación en los navegadores es muy irregular y no lo contemplaremos por el momento. 



• Imágenes de mapa de bits o bitmap que, tal como nos sugiere su nombre se construyen describiendo cada uno de los puntos que componen la imagen y llevan, por tanto, información acerca de la posición absoluta y el color de cada uno de ellos. Podríamos decir que cada punto sería la tesela de un mosaico con sus propias características. La ventaja que presenta este formato es la posibilidad de recoger una amplísima gama tonal, por lo que es el tipo adecuado para representar imágenes captadas de la realidad. A cambio, la variación de tamaño supondrá modificaciones en la calidad, ya que el número de celdas que forman la imagen permanece invariable, por lo que un aumento del tamaño hace que el único recurso posible sea ampliar el tamaño de cada una de ellas. Podemos deducir por lo dicho anteriormente que su tamaño es muy grande, ya que aquí sí que tenemos información de cada uno de los puntos que forman la imagen. Dentro de este tipo se encuentran muchos formatos, algunos de los cuales son soportados directamente por los navegadores, siendo pues el tipo de imágenes con las que vamos a trabajar en el curso.

Resolución del monitor

A grandes rasgos la resolución del monitor viene determinada por dos variables:

• El tamaño de la "celda", al que se denomina pitch dot y que, en los monitores actuales, es habitualmente de 0,28 mm. Dado que la imagen que vemos está compuesta por puntos adyacentes de diferentes colores, cuanto más pequeños sean dichos puntos obtendremos una mayor sensación de continuidad.
  
  
• El número de puntos que es capaz de enviar a la pantalla la tarjeta gráfica del ordenador. Este parámetro depende de la cantidad de memoria de la que disponga la tarjeta para hacer los cálculos necesarios y de la propia capacidad de la pantalla para representar la información recibida. Cada pareja de tarjetas gráfica y monitor es capaz de presentar un rango de resoluciones, cuya elección queda a criterio del usuario. Actualmente la resolución más habitual es, aproximadamente en proporciones similares, de 800 puntos horizontales por 600 puntos verticales, o 1024x768, aunque con tendencia hacia esta última a medida que los tamaños de pantalla se hacen mayores y las tarjetas gráficas más potentes.

La variación del número de puntos o píxeles influirá en el tamaño relativo de las imágenes dentro de la pantalla. Si establecemos que nuestra pantalla va a ser un mosaico de 800 x 600, una imagen que ocupe un rectángulo de 640x480 píxeles que se situara a partir del vértice superior izquierdo, dejaría libre una franja a su derecha y otra en la parte inferior. Si pretendemos mostrar esa misma imagen en una pantalla con una resolución de 640x480 la llenará por completo. La imagen no ha variado de tamaño, lo que se ha modificado es el tamaño de cada una de las "baldosas" que componen el mosaico.

Resolución de la imagen

Es un concepto relacionado con el anterior y tiene una importante repercusión a la hora de adecuar las imágenes a la pantalla para que su transmisión sea lo más rápida posible. Recurriremos a un ejemplo práctico para explicarlo.

Supongamos que disponemos de un escáner para capturar una imagen. Introducimos sobre la bandeja una foto cuyo tamaño es de 10 x 15 cm (aproximadamente unas 4 x 6 pulgadas).

Inicio el trabajo de captura y, como mi escáner me lo permite, capturo la imagen a 300 puntos por pulgada. Eso quiere decir que por cada pulgada real de foto, el dispositivo óptico del escáner se encargará de pintar 300 puntos en la imagen electrónica. Un simple cálculo me hace darme cuenta de que mi imagen formará un rectángulo de 1200 x 1800 píxeles una vez escaneada, ya que la imagen original era de 4 x 6 pulgadas.

¿Cabrá la imagen en la pantalla? Está claro que no, porque lo más lógico es que mi pantalla esté configurada para mostrar 800 puntos de anchura y 600 de altura  o 1024 x 768 que es bastante menos de lo que necesitamos.

Entonces, ¿cuál será la resolución adecuada para mostrar una imagen en pantalla de forma que su tamaño corresponda aproximadamente con el original en papel? Para responder a esta pregunta vamos a recurrir a una simple demostración aplicando el teorema de Pitágoras.

Vamos a tomar como referencia un monitor de 14". Eso quiere decir que la diagonal del mismo medirá 14".

La proporción que existe entre el ancho y el alto de la pantalla es de 4 : 3, por lo que podemos decir que la anchura física de la pantalla es de 4x" y su altura de 3x". 

Con esos datos tenemos la información necesaria para poder aplicar el teorema de Pitágoras ya que conocemos la medida de la hipotenusa y hemos podido establecer la proporción entre los catetos.

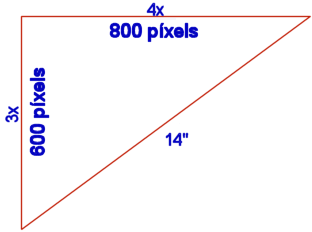
Así pues nos bastará con despejar el valor de la x.

h² = C² + c²
14² = (4x)² + (3x)²
196 = 16x² + 9x²
196 / 25 = x²

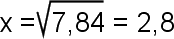
Una vez comprobado que x=2,8 podemos fijar las medidas de ancho y alto de la pantalla que quedarían en 11,2 " y 8,4" respectivamente.

Tomemos ahora, por ejemplo, el ancho de la pantalla. Si la resolución está fijada a 800x600, ¿cuántos píxeles se nos mostrarán en cada pulgada de pantalla?. Como ya sabemos que el ancho es de 11, 2" basta con una simple división para que nos resulte 800 : 11,2 = 71,428 píxeles por pulgada (ppp). Dado que el ancho que hemos calculado es teórico y es algo más grande que la realidad, se opta por redondear ese resultado a 72 ppp que será una cifra que encontrarás en multitud de programas como resolución estándar para la pantalla. El mismo resultado habríamos obtenido en caso de haber hecho el cálculo sobre la altura de la pantalla.

A continuación se muestra una tabla resumen sobre las resoluciones ppp aplicables para que la imagen en pantalla coincida con el tamaño original en papel.

Profundidad de color

Un bit es la unidad mínima de información digital. Se trata de una magnitud binaria que puede reflejar dos valores: 0 o 1. Si creamos una imagen con dos colores bastará con un sólo bit por cada píxel para indicar el color que habrá que aplicar.

Si dibujáramos la letra T utilizando únicamente dos colores, blanco para el fondo y negro para el primer plano, el mapa que se formaría sería similar al que se muestra en la imagen de la derecha, en el que cada uno de los puntos que forma la imagen podría representarse con un solo bit, ya que un cero nos indicaría que el píxel es del color del fondo y un uno marcaría que hay que colorear el píxel con el color del primer plano.

Si en lugar de un bit utilizáramos dos para indicar el color de cada píxel pasaríamos de tener como valores posibles el 0 y el 1 a disponer de los valores 00, 01, 10 y 11, esto es cuatro posibles colores.

Si reconsideramos por un instante el hecho de que la información digital se basa en un sistema binario nos daremos cuenta de que podríamos calcular fácilmente el número de colores posibles según la cantidad de bits que utilicemos para indicar el número de colores posibles en cada píxel. Tomando el 2 como base y aplicándole el número de bits como exponente obtendremos el número de colores que se logra en cada caso. A esto es a lo que llamaremos profundidad de color y puede sintetizarse en la siguiente tabla:

Es probable que te preguntes por qué no hemos completado la tabla si hemos hablado de imágenes de 16 millones de colores. De alguna forma tienes razón puesto que se trata de imágenes de 24 bits, pero se trata realmente de la combinación de tres imágenes de 8 bits correspondientes a los colores básicos. Si combinamos 256 posibles tonos de rojo con otros tantos de verde y los mismos de azul conseguiremos un total de 256³ = 16777216 colores que es, lógicamente el mismo resultado que obtendríamos si calculáramos 2²⁴ = 16777216

Si lees con atención este apartado es posible que deduzcas que un aumento de la profundidad de color llevará aparejado un aumento del tamaño de la imagen. Si tomamos en cuenta la cantidad de memoria requerida para construir la imagen es correcta la deducción, pero no podemos aplicarlo cuando se trata de considerar el tamaño de almacenamiento del archivo. Para guardar una imagen se aplican, según el tipo de archivo que utilicemos, algoritmos de compresión que reducen considerablemente la cantidad de bits almacenados.