5.1.8. Ejemplo de cálculo del par motor en sistema lineal
Ejemplo 1. Encontrar el par del motor necesario para accionar el sistema mostrado en la figura 5.20, que representa el eje X de un sistema de posicionamiento cartesiano X-Y-Z. El accionamiento se realiza con un motor de 1.8º por paso, unido mediante un acoplamiento elástico de aluminio directamente a un husillo, con un paso de 10 mm. La sujeción está formada por un soporte con rodamientos con precarga de 22 Kg, en el otro extremo se dispone un rodamiento sin precarga. El elemento de guiado está formado por una guía lineal de 20 mm, con un patín por rodamientos a bolas sin precarga. La masa de todos los elementos de los ejes Y-Z apoyados sobre el eje X es de 10 Kg. La fuerza de trabajo necesaria para accionar la herramienta de corte es de 200 N. La aceleración máxima es 0.5 m/s2.
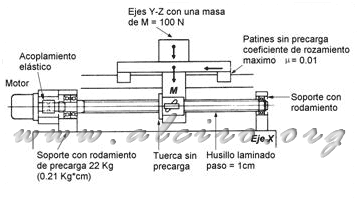
Figura 5.20. Eje X de un sistema de posicionamiento lineal X-Y-Z.
Otros datos:
Jmotor = 150 g*cm2
Lhusillo = 0.5 m
μ = 0.01
El par necesario para accionar el sistema se reparte en primar lugar en el par de arranque de los rodamientos con precarga. El fabricante nos indica que para un soporte de eje de 12 mm y un rodamiento con precarga de 22 Kg el par de arranque es de 20.59*10-3 N*m.
La fuerza Fc necesaria para mover la carga con un coeficiente de fricción entre patín y guía de μ = 0.01 es μ*M (resistencia a la rodadura) que sumada con la fuerza de trabajo F
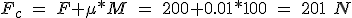(5.39)
la resistencia a la rodadura es prácticamente despreciable, ya que el echo de utilizar guías y patines a bolas proporciona un coeficiente de fricción muy bajo, a esto se suma el poco peso del sistema. Transformando la fuerza a un par mediante un husillo de paso 10 mm y un rendimiento del 90 %.
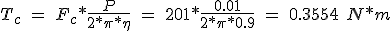(5.40)
La tuerca del husillo es sin precarga, por lo que las pérdidas de par en éstas se consideran despreciables. El par total del motor necesario para mover la carga o desplazarla a velocidad constante es:
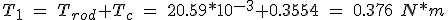(5.41)
Si el sistema se acelera, se tiene que realizar un análisis de las inercias. De un husillo de 0.5 m de longitud y un diámetro de 16 mm,
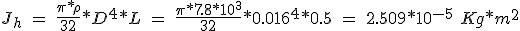(5.42)
también se puede obtener el momento de inercia a partir de la gráfica de la figura 5.19, de la intersección entre la longitud de 50 cm y el diámetro del husillo de 16 mm, dando 0.25 Kg*cm2. La inercia del acoplamiento elástico entre el eje del rotor y el husillo se puede despreciar ya que éste es de aluminio y no representa un incremento apreciable. La inercia derivada de la carga viene determinada según la expresión:
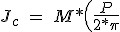^2\ =\ 10*\left( \frac{0.01}{2*\pi} \right)^2\ =\ 2.533*10^{-5}\ Kg*m^2 "J_c\ =\ M*\left( \frac{P}{2*\pi } \right)^2\ =\ 10*\left( \frac{0.01}{2*\pi} \right)^2\ =\ 2.533*10^{-5}\ Kg*m^2")
(5.43)
si la inercia del rotor del motor es de 150 gm*cm2, la inercia total del sistema es.
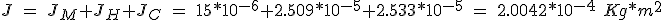(5.44)
Aplicando la ecuación 5.1 para una aceleración lineal de la carga de 0.5 m*s-2 (el motor acelera a 100*Π radianes/s2), se obtiene el par del motor necesario para desplazar y acelerar el sistema.
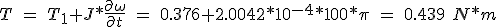(5.45)
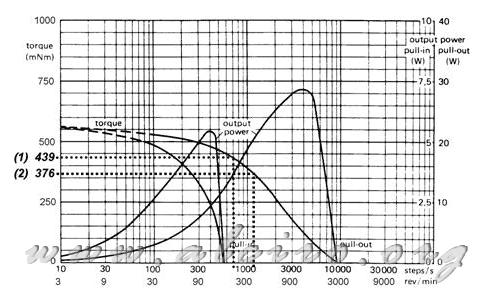
Figura 5.21. Curvas caracteísticas de un motor híbrido de 1,8º con la situación del par necesario para acelerar el sistena a 50 cm/s2 (1), y el de velocidad constante (2).
Si se sitúa el par obtenido para acelerar el eje sobre las características de par/velocidad del motor mostradas en la figura 5.21, se obtiene la razón de pasos máxima de 700 pasos/s que puede alcanzar el motor manteniendo esta situación. Situando en la misma gráfica el par a velocidad constante obtenemos una razón de pasos de 1100 pasos/s para este estado.
