Acceleration of stepper motors, Plotter Router Fresadora CNC, alciro

User: alciro User

Original Translate to: Deutsch English Français 中文

Plotter Router Fresadora CNC

Anemómetro

Domótica sencilla, fácil y económica

Impresora alciro-3D printer

microHomeLan.net

microPLC para arduino

Plotter Router Fresadora CNC

1. MOTOR STEP BY STEP (STEP MOTOR)

1.1. Permanent magnet motors
1.2. Stepper motors, variable reluctance

1.3. Hybrid Stepper Motors

1.3.1. Hybrids of two and four phases
1.3.2. Hybrids of three and five stages

1.4. Comparison of different types of stepper motors

2. CHARACTERISTICS OF STEPPER MOTORS

2.1. Static characteristics

2.1.1. Holding torque (Holding torque)
2.1.2. Static position error

2.1.3. Excitation sequences

2.1.3.1. Variable reluctance motors
2.1.3.2. Hybrid engines
2.1.3.3. Microstep sequence

2.2. Dynamic Characteristics

2.2.1. Curves / torque / frequency
2.2.2. Relationship between the dynamic torque and static torque
2.2.3. Mechanical Resonance
2.2.4. Compensating mechanical inertia (dampers)

2.2.5. High speed operation

2.2.5.1. Model of a hybrid stepper motor
2.2.5.2. Calculation of dynamic torque (pull out)

4. ENGINE POWER STEP BY STEP

4.1. Excitation sequences

4.1.1. Sequence of two active phases (full step)
4.1.2. Sequence of an active phase (wave-wave excitation)
4.1.3. Half-step sequence (half step)
4.1.4. Excitation sequence for a variable reluctance motor
4.1.5. Excitation sequence in microstep stepper motors

4.2. Stepper motor bipolar and unipolar

4.2.1. Relationship between torque and bipolar and unipolar excitation
4.2.2. Stepper Motors 8-wire

4.3. Power amplifiers (Drivers)

4.3.1. Problems with Drivers

4.3.1.1. Suppression circuits

4.3.2. Constant voltage feeding

4.3.2.1. Improvement additional resistance voltage feeding

4.3.3. Stepper motor control for power

4.3.4. Bipolar chopper control in H-bridge

4.3.4.1. H-bridge for a two-phase motor.
4.3.4.2. Chopper phase and inhibition

4.3.5. Choosing the type of chopper

4.3.5.1. Ripple Current
4.3.5.2. Losses in the motor
4.3.5.3. Dissipation in the bridge
4.3.5.4. Minimum current

4.3.6. Types of current control

4.3.6.1. Pulse width modulation (Pulse Width Modulation)
4.3.6.2. Fixed stop time (Frequency Modulation switching control)

5. TORQUE CHARACTERISTICS AND PULSE INTERVALS

5.1. Dynamic equations and acceleration

5.1.1. Dynamic equations
5.1.2. Friction torque

5.1.3. Acceleration of stepper motors

5.1.3.1. Slowdown in stepper motors
5.1.3.2. Limitations of the analysis of acceleration
5.1.3.3. Need to optimize acceleration

5.1.4. Optimal velocity profile

5.1.4.1. Velocity profile equations
5.1.4.2. Example of calculating the velocity profile
5.1.4.3. Considerations of the velocity profile

5.1.5. Loads connected to the engine through transmission elements

5.1.5.1. Transmitted by belts and gears
5.1.5.2. Lifting
5.1.5.3. Moving objects using tape
5.1.5.4. Linear motion by worm and gear

5.1.6. Performance of a screw
5.1.7. Friction, torque and inertia
5.1.8. Example of calculating the torque in linear system
5.1.9. Example of calculating torque motor pull-in start

5.2. Determination of time and pulse interval

5.2.1. Considerations on the characteristics of pull-in
5.2.2. Theory of linear acceleration pulse intervals

6. STAGE OF POWER AND CONTROL CIRCUIT

6.1. Amplifier

6.1.1. Driver

7. ALGORITHMS AND CONTROL PROGRAM

7.1. Instructions and communication

7.1.1. Control Commands

7.1.1.1. Command parameters control
7.1.1.2. Shares of control commands

Technical Datasheets

5.1.3. Acceleration of stepper motors

Because the engine can not start at the maximum speed of work, since it does not have sufficient torque to pull the load with the inertia that is starting at high speed, you have to run at a low rate of subsequent steps accelerate gradually until reaching the maximum operating speed. Similarly one has to operate to stop the engine, based on a high speed slows down to the unemployment rate without losing steps.

(1) Linear acceleration. When the term of the viscous friction is negligible, then equation 5.1 can be expressed:

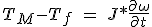$T_M-T_f\ =\ J*\frac{\partial \omega}{\partial t}$ (5.4)

If the motor torque is constant and only considered the range of speed, integration of Equation 5.4 yields:

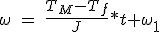$\omega \ =\ \frac{T_M-T_f}{J}*t+\omega_{1}$ (5.5)

or frequency of steps

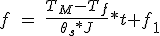$f \ =\ \frac{T_M-T_f}{\theta _s*J}*t+f_{1}$ (5.6)

where

Ω ₁ = angular velocity before the acceleration start
f ₁ = frequency of steps before you start acceleration.

Example 1. What is the motor torque required to accelerate a load inertia of 10 ^-4 m ² kg * ₁ = 100 Ω to Ω ₂ = 300 rad * s ^-1 for 0.1 s, T _f is 0.05 N * m?

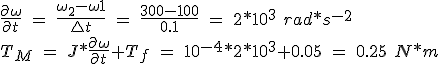$\frac{\partial \omega }{\partial t}\ =\ \frac{\omega _{2}-\omega {1}}{\bigtriangleup t}\ =\ \frac{300-100}{0.1}\ =\ 2*10^3\ rad*s^{-2}\\ T_M\ =\ J*\frac{\partial \omega }{\partial t}+T_f\ =\ 10^{-4}*2*10^3+0.05\ =\ 0.25\ N*m$ (5.7)

Example 2. What is the motor torque required to accelerate an inertial load of 2 * 10-4 Kg * m ² = 500 Hz f ₁ f ₂ = 1500 Hz for 50 ms? Friction loads are negligible. The pitch angle is θ _s = 1.8 ° = 3.1416 * 10-2 rad.

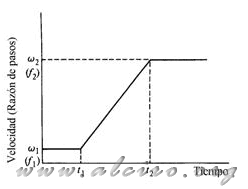
Figure 5.3. Ω1 linear acceleration to ω2 for t1-t2

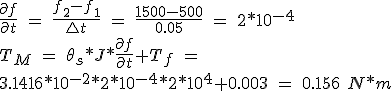$\frac{\partial f}{\partial t}\ =\ \frac{f_{2}-f_{1}}{\bigtriangleup t}\ =\ \frac{1500-500}{0.05}\ = \ 2*10^{-4}\\T_M\ =\ \theta _s*J*\frac{\partial f}{\partial t}+T_f\ =\ \\3.1416*10^{-2}*2*10^{-4}*2*10^4+0.003\ =\ 0.156\ N*m$ (5.8)

Example 3. What is the maximum acceleration of an inertia load of 10-4 Kg * m ² driven by a motor with a torque of 0.2 N * m? Friction loads are negligible. The pitch angle is 2 º = 3419 * 10-2 rad.

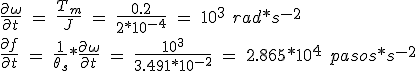$\frac{\partial \omega }{\partial t}\ =\ \frac{T_m}{J}\ =\ \frac{0.2}{2*10^{-4}}\ =\ 10^3\ rad*s^{-2}\\ \frac{\partial f}{\partial t}\ =\ \frac{1}{\theta _s}*\frac{\partial \omega }{\partial t}\ =\ \frac{10^3}{3.491*10^{-2}}\ =\ 2.865*10^4\ pasos*s^{-2}$ (5.9)

(2) exponential acceleration. When the viscous friction torque is not negligible the equation can be written as:

$\theta _s*J*\frac{\partial f}{\partial t}+\theta _s*D*f-(T_M-T_f)\ =\ 0$ (5.10)

If the motor torque is not a function of the ratio of steps or speed, the solution to this differential equation is:

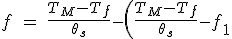$f\ =\ \frac{T_M-T_f}{\theta _s}-\left( \frac{T_M-T_f}{\theta _s}-f_{1} \right)*e^{-(\frac{D}{J})*t}$ (5.11)

where

f ₁ = ratio of steps at the beginning.

So, the reason for the positive acceleration decreases with the ratio of steps. This type of acceleration is referred to as (exponential acceleration).

When the motor torque TM is decreased with the ratio of steps in a linear fashion, similar to (5.12), the maximum acceleration possible depends on the exponential.

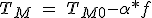$T_M\ =\ T_{M0}-\alpha *f$ (5.12)

Share |