Accélération de moteurs pas à pas, Plotter Router Fresadora CNC, alciro

User: alciro User

Original Translate to: Deutsch English Français 中文

Plotter Router Fresadora CNC

Anemómetro

Domótica sencilla, fácil y económica

Impresora alciro-3D printer

microHomeLan.net

microPLC para arduino

Plotter Router Fresadora CNC

1. ÉTAPE PAR ÉTAPE AUTOMOBILE (MOTEUR PAS A PAS)

1.1. moteurs à aimants permanents
1.2. moteurs pas à pas, à réluctance variable

1.3. Moteurs pas à pas hybrides

1.3.1. Les hybrides de deux et quatre phases
1.3.2. Hybrides de trois et cinq étapes

1.4. Comparaison des différents types de moteurs pas à pas

2. Caractéristiques des moteurs STEPPER

2.1. Caractéristiques statiques

2.1.1. Couple de maintien (Couple de maintien)
2.1.2. erreur de position statique

2.1.3. Excitation des séquences

2.1.3.1. moteurs à réluctance variable
2.1.3.2. Les moteurs hybrides
2.1.3.3. séquence Microstep

2.2. Caractéristiques dynamiques

2.2.1. Curves / couple / fréquence
2.2.2. Relations entre le couple dynamique et statique du couple
2.2.3. Mechanical Resonance
2.2.4. Compensation inertie mécanique (amortisseurs)

2.2.5. Opération à grande vitesse

2.2.5.1. Modèle d'un moteur pas à pas hybrides
2.2.5.2. Calcul du couple dynamique (retirer)

4. ÉTAPE PAR ÉTAPE PUISSANCE

4.1. Excitation des séquences

4.1.1. Séquence de deux phases actives (pas complet)
4.1.2. Déroulement d'une phase active (excitation onde-onde)
4.1.3. Demi-étape de la séquence (demi-pas)
4.1.4. Séquence d'excitation pour un moteur à réluctance variable
4.1.5. Séquence d'excitation dans les micropas moteurs pas à pas

4.2. bipolaires et unipolaires moteur pas à pas

4.2.1. Relation entre le couple et d'excitation bipolaires et unipolaires
4.2.2. Moteurs pas à pas 8 fils

4.3. Les amplificateurs de puissance (Pilotes)

4.3.1. Problèmes avec les pilotes

4.3.1.1. circuits répression

4.3.2. Constant tension d'alimentation

4.3.2.1. Amélioration d'alimentation de tension supplémentaire résistance

4.3.3. commande de moteur pas à pas pour le pouvoir

4.3.4. Commande du hacheur bipolaire en pont en H

4.3.4.1. H-bridge pour un moteur à deux phases.
4.3.4.2. Phase de Chopper et l'inhibition

4.3.5. Choisir le type de chopper

4.3.5.1. Courant d'ondulation
4.3.5.2. Les pertes dans le moteur
4.3.5.3. Dissipation dans le pont
4.3.5.4. Courant minimum

4.3.6. Types de contrôle de courant

4.3.6.1. Pulse Width Modulation (Pulse Width Modulation)
4.3.6.2. Temps d'arrêt fixe (modulation de fréquence de commutation de commande)

5. Caractéristiques de couple et des intervalles d'impulsion

5.1. équations dynamiques et l'accélération

5.1.1. équations dynamiques
5.1.2. de couple à friction

5.1.3. Accélération de moteurs pas à pas

5.1.3.1. Ralentissement de moteurs pas à pas
5.1.3.2. Limites de l'analyse de l'accélération
5.1.3.3. Nécessité d'optimiser l'accélération

5.1.4. profil de vitesse optimale

5.1.4.1. équations de profil de vitesse
5.1.4.2. Exemple de calcul du profil de vitesse
5.1.4.3. Considérations du profil de vitesse

5.1.5. Charge reliée au moteur par le biais des éléments de transmission

5.1.5.1. Transmis par des courroies et engrenages
5.1.5.2. De levage
5.1.5.3. Les objets en mouvement en utilisant du ruban
5.1.5.4. mouvement linéaire par vis sans fin et engrenages

5.1.6. Performance d'une vis
5.1.7. Friction, le couple et l'inertie
5.1.8. Exemple de calcul du couple dans le système linéaire
5.1.9. Exemple de calcul de couple moteur de traction dans le démarrage

5.2. Détermination du temps et l'intervalle d'impulsion

5.2.1. Considérations sur les caractéristiques de pull-in
5.2.2. Théorie des intervalles de pouls accélération linéaire

6. STADE DE CIRCUIT D'ALIMENTATION ET DE CONTRÔLE

6.1. Amplificateur

6.1.1. Driver

7. ALGORITHMES ET PROGRAMME DE COMMANDE

7.1. Instructions et de la communication

7.1.1. Commandes de contrôle

7.1.1.1. paramètres de commande de contrôle
7.1.1.2. Actions des commandes de contrôle

Fiches techniques

5.1.3. Accélération de moteurs pas à pas

Parce que le moteur ne peut pas démarrer à la vitesse maximale de travail, car il n'a pas un couple suffisant pour tirer la charge avec l'inertie qui est en train à grande vitesse, vous avez à courir à un faible taux d'étapes ultérieures accélérer progressivement jusqu'à atteindre la vitesse maximale de fonctionnement. De même, on doit opérer pour arrêter le moteur, basée sur une vitesse élevée ralentit le taux de chômage sans perdre étapes.

(1) l'accélération linéaire exprimé. Lorsque la durée de la friction visqueuse est négligeable, alors l'équation 5.1 peut être:

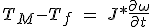$T_M-T_f\ =\ J*\frac{\partial \omega}{\partial t}$ (5.4)

Si le couple du moteur est constante et ne considère que l'éventail de la vitesse, l'intégration de l'équation 5.4 donne:

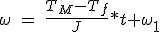$\omega \ =\ \frac{T_M-T_f}{J}*t+\omega_{1}$ (5.5)

ou la fréquence des mesures

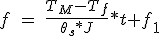$f \ =\ \frac{T_M-T_f}{\theta _s*J}*t+f_{1}$ (5.6)

où

Ω ₁ = vitesse angulaire avant le début d'accélération
f ₁ = fréquence des étapes avant de commencer à l'accélération.

Exemple 1. Quel est le couple moteur nécessaire pour accélérer une inertie de la charge de 10 ^-4 m ² kg * ₁ = 100 Ω à Ω ₂ = 300 * rad s ^-1 pendant 0,1 s, T _f est de 0,05 N * m?

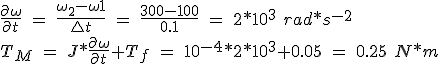$\frac{\partial \omega }{\partial t}\ =\ \frac{\omega _{2}-\omega {1}}{\bigtriangleup t}\ =\ \frac{300-100}{0.1}\ =\ 2*10^3\ rad*s^{-2}\\ T_M\ =\ J*\frac{\partial \omega }{\partial t}+T_f\ =\ 10^{-4}*2*10^3+0.05\ =\ 0.25\ N*m$ (5.7)

Exemple 2. Quel est le couple moteur nécessaire pour accélérer une force d'inertie de 2 * 04/10 Kg * m ² = 500 Hz f ₁ f ₂ = 1500 Hz pendant 50 ms? charges de friction sont négligeables. L'angle de tangage θ _s = est de 1,8 ° = 3,1416 * 2.10 rad.

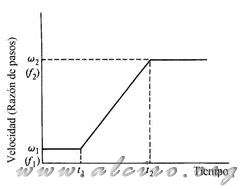
Figure 5.3. Ω1 accélération linéaire à ω2 pour T1-T2

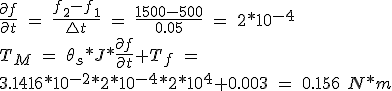$\frac{\partial f}{\partial t}\ =\ \frac{f_{2}-f_{1}}{\bigtriangleup t}\ =\ \frac{1500-500}{0.05}\ = \ 2*10^{-4}\\T_M\ =\ \theta _s*J*\frac{\partial f}{\partial t}+T_f\ =\ \\3.1416*10^{-2}*2*10^{-4}*2*10^4+0.003\ =\ 0.156\ N*m$ (5.8)

Exemple 3. Quelle est l'accélération maximale d'une charge d'inertie de 10-4 Kg * m ² entraîné par un moteur avec un couple de 0,2 N * m? charges de friction sont négligeables. L'angle d'attaque est de 2 º = 3419 * 2.10 rad.

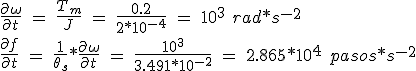$\frac{\partial \omega }{\partial t}\ =\ \frac{T_m}{J}\ =\ \frac{0.2}{2*10^{-4}}\ =\ 10^3\ rad*s^{-2}\\ \frac{\partial f}{\partial t}\ =\ \frac{1}{\theta _s}*\frac{\partial \omega }{\partial t}\ =\ \frac{10^3}{3.491*10^{-2}}\ =\ 2.865*10^4\ pasos*s^{-2}$ (5.9)

(2) l'accélération exponentielle. Lorsque le couple de frottement visqueux n'est pas négligeable, l'équation peut s'écrire:

$\theta _s*J*\frac{\partial f}{\partial t}+\theta _s*D*f-(T_M-T_f)\ =\ 0$ (5.10)

Si le couple du moteur n'est pas une fonction du rapport d'étapes ou de la vitesse, la solution de cette équation différentielle est:

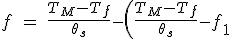$f\ =\ \frac{T_M-T_f}{\theta _s}-\left( \frac{T_M-T_f}{\theta _s}-f_{1} \right)*e^{-(\frac{D}{J})*t}$ (5.11)

où

f ₁ = rapport d'étapes au début.

Donc, la raison de l'accélération positive diminue avec le rapport d'étapes. Ce type d'accélération est dénommé (accélération exponentielle).

Lorsque le couple moteur TM est réduite par le rapport d'étapes de façon linéaire, similaire à (5.12), l'accélération maximale possible dépend de la exponentielle.

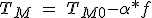$T_M\ =\ T_{M0}-\alpha *f$ (5.12)

Share |