5.1.4.2. Exemple de calcul du profil de vitesse
Exemple: moteur pas à pas a une longueur de 15 étapes degré et une caractéristique couple / vitesse de traction-out comme le montre la figure 5.8, il est proposé d'accélérer une inertie de la charge de 2 kg * 10-4 m * 2 et une paire de 0,1 N * m. Obtenir la courbe de profil de vitesse pour accélérer le système optimal.
Le pull-out raison de ce système est de 435 étapes * s-1, de sorte à ce rythme, l'arrachement de couple des moteurs est égale à la charge de couple.
La variation de l'arrachement de couple avec la vitesse peut être assimilée à une ligne droite, comme indiqué par la ligne pointillée à la figure 5.8. T (f) est approximatif à la fonction:
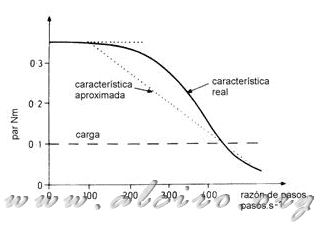
Figure 5.8. Caractéristiques de deux gigogne montrant l'approximation linéaire.
\ =\ 0.35\ N*m\ \ \ 0<f<100\ pasos*s^{-1}\\ y\ =\ 0.426-0.00075*f\ N*m\ \ 100<f<435\ pasos*s^{-1}\\ T_L(f)=0.1\ N*m "Tirez-en montrant l'approximation linéaire")
(5.20)
Pour des raisons d'étapes jusqu'à 100 étapes * s -1:
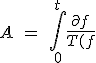-T_L(f)}\ =\ \ \int_{0}^{t}\frac{\partial f}{0.25}\ =\ 4*f\ (N*m*s)^{-1} "Pour des raisons d'étapes jusqu'à 100 chiffons * s-1")
(5.21)
La longueur de pas est de 15 degrés = 0,262 radians = 2 π / * n * p. D'après l'équation 5.21, le temps nécessaire pour atteindre le ratio de l'étape f est:
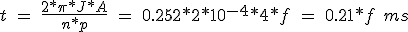(5.22)
Ainsi, la vitesse augmente linéairement avec le temps jusqu'à atteindre les 100 marches * s -1, atteint après 21 ms.
Pour des raisons de passage entre 100 et 435 étapes * s -1:
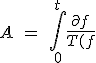-T_L(f)}\ =\ \ \int_{0}^{100}\frac{\partial f}{0.25}+\int_{100}^{f}\frac{\partial f}{0.426-0.00075*f}\\ =\ 9630-1333*log(1305-3*f)\ (N*m*s)^{-1} "Pour des raisons de chiffons entre 100 et 435 étapes * s-1")
(5.23)
D'après l'équation 5.19, le temps nécessaire pour atteindre le ratio d'étapes dans la gamme de 100-435 étapes * s -1 est donc:
![t\ =\ \frac{2*\pi *J*A}{n*p}\ =\ 0.0262*2*10^{-4}*[9630-1333*log(1305-3*f)]\\ =\ 0.503-0.0679*log(1305-3*f)\ s](http://www.alciro.org/cgi/tex.cgi?t\ =\ \frac{2*\pi *J*A}{n*p}\ =\ 0.0262*2*10^{-4}*[9630-1333*log(1305-3*f)]\\ =\ 0.503-0.0679*log(1305-3*f)\ s "Temps nécessaire pour atteindre le ratio de 100 à 435 mesures")
(5.24)
