2.2.5.2. Calcul du couple dynamique (retirer)
Maintenant, nous devons établir la relation entre la composante fondamentale de la tension et de courant en phase avec la paire. La sortie de puissance mécanique de la phase est simplement le produit du courant à travers la phase et la tension induite.
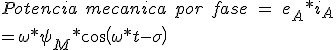*I.cos(\omega *t-\sigma -a)\\ =\frac{\omega *\psi _M*I*cos(a)}{2}+\frac{\omega *\psi _M*I*cos(2*\omega *t-2*\sigma -a)}{2}) (3.25)
(3.25)
D'après l'équation 3.25 Les composants qui varient au fil du temps n'ont aucun intérêt et est seulement nécessaire d'évaluer le premier terme. Pour un hybride de deux phases, la puissance mécanique totale est la suivante:
) (3.26)
(3.26)
l'Icos terme (a) est éliminé de cette équation avec la construction de la ligne AA 'dans le diagramme vectoriel (Figure 3.24) à un angle de la ZI vecteur.

Figure 3.23. Construction du diagramme de vecteur pour l'expression cos * I (a).
L'expression de la longueur de la ligne AA 'est la projection m ωδ vecteurs, V et ZI sur la ligne:
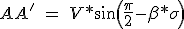\ =\ \omega *\psi _M*cos(\beta )+Z*I*cos(\alpha ))
ensuite.
\ =\ \frac{V*sin(\frac{\pi }{2}-\beta +\sigma)-\omega *\psi _M*cos(\beta ) }{Z}\\ =\ \frac{V*cos(\beta -\sigma)-\omega *\psi _M*cos(\beta ) }{Z}) (3.27)
(3.27)
En substituant I * cos (α) de l'équation 3.27 dans l'équation 3.26.
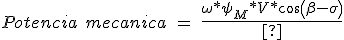-\omega ^2*{\psi _M}^2*cos(\beta ) }{Z}) (3.28)
(3.28)
Mais la puissance mécanique est équivalente à la paire de produit pour la vitesse. De l'équation 3.18 est la vitesse ω / d et donc:
![l'équation de couple d'un moteur pas à pas hybrides Par\ =\ \frac{Potencia}{Velocidad}\ =\ \frac{d*[\psi _M*V*cos(\beta -\sigma)-\omega *{\psi _M}^2*cos(\beta )] }{Z}](http://www.alciro.org/cgi/tex.cgi?Par\ =\ \frac{Potencia}{Velocidad}\ =\ \frac{d*[\psi _M*V*cos(\beta -\sigma)-\omega *{\psi _M}^2*cos(\beta )] }{Z}) (3.29)
(3.29)
pour trouver les paramètres à vitesse fixe la seule variable dans l'équation 3.29 est l'angle de charge (σ). La variation de ce qui est cohérent avec la charge, le couple du moteur et la charge sont égaux. Lorsque la charge appliquée, l'angle de charge est semblable à l'expression du couple. Analyse de l'équation 3.29 Le couple maximum est atteint lorsque β = σ, alors:
![Equation gigogne couple d'un moteur pas à pas Par_{(Pull\ out)}\ =\ \frac{d*[\psi _M*V-\omega *{\psi _M}^2*cos(\beta )] }{Z}\\ =\frac{d*\psi _M*V}{\left( R^2+\omega ^2*L^2 \right)^{1/2}}-\frac{d*\omega * {\psi _M}^2*R}{\left( R^2+\omega ^2*L^2 \right)}](http://www.alciro.org/cgi/tex.cgi?Par_{(Pull\ out)}\ =\ \frac{d*[\psi _M*V-\omega *{\psi _M}^2*cos(\beta )] }{Z}\\ =\frac{d*\psi _M*V}{\left( R^2+\omega ^2*L^2 \right)^{1/2}}-\frac{d*\omega * {\psi _M}^2*R}{\left( R^2+\omega ^2*L^2 \right)}) (3.30)
(3.30)
Une vitesse de courbe de couple-bas équivaut à retirer (m δψ V) / R. Cette paire peut également être déduite par les caractéristiques de couple statique, selon la méthode décrite dans la section 3.2.2, le flux magnétique (ψm) peut être exprimée selon les termes du pic de couple statique.
Lorsque le rapport de l'augmentation des mesures, le couple dynamique (pull out) est réduite progressivement au niveau zéro à une certaine vitesse ω m (Figure 3.25).
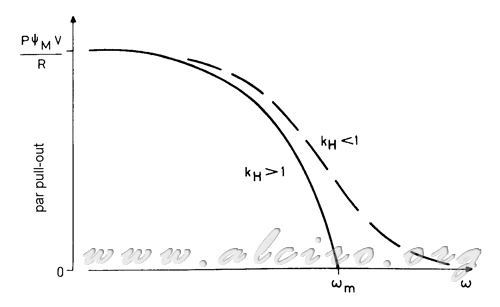
Figure 3.25. Waveform couple / vitesse obtenue dans le calcul de l'arrachement de couple pour un moteur pas à pas hybride.
Pour une autre réponse, la propriété est asymptotique à l'axe T = 0, la paire est tangente à zéro à un rapport d'étapes infinie.
Assimiler l'équation 3,30 à zéro quelques obtenir la vitesse maximale ωm:
^{1/2}}-\frac{d*\omega * {\psi _M}^2*R}{\left( R^2+\omega ^2*L^2 \right)}\ =\ 0)
et, par conséquent;
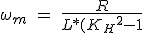^{1/2}}) (3.31)
(3.31)
être KH = WMR / VL moteur constant. Pour l'équation 3.31 La valeur réelle de la fréquence maximale de fonctionnement ne peut être obtenu que si KH est supérieur à l'unité, dans ce cas, la racine carrée du dénominateur peut être évaluée. Le taux maximal d'étapes de l'équation 3.31 est la suivante:
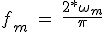 (3.32)
(3.32)
La fréquence de fonctionnement maximale est obtenue à partir de l'équation 3.31, est proportionnelle à la résistance totale de la phase (R), si le moteur doit fonctionner à haute vitesse, le circuit de puissance doit inclure une forte résistance.
Pour le choix d'un moteur doit travailler à une vitesse élevée est souhaitable que la valeur de KH est aussi faible que possible, de sorte que le dénominateur de l'expression pour obtenir la fréquence maximale est réduite au minimum.







