5.1.4.1. équations de profil de vitesse
\ =\ T_L(f)+J*\left( \frac{\partial^2 \theta }{\partial t^2} \right)) (5.15)
(5.15)
Pour un moteur n-phase avec les dents du rotor et p la longueur des étapes est de 2 π * / p * n, et le rapport d'étapes est liée à la vitesse du rotor:
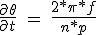 (5.16)
(5.16)
substituant l'équation 5.15 dans la 5.15
![En substituant les équations T(f)\ =\ T_L(f)+\left( J*\frac{2*\pi }{n*p}\right)*\frac{\partial f}{\partial t}\\ \frac{\partial f}{\partial t}\ =\ \left[ T(f)-T_L(f) \right]*\frac{n*p}{2*\pi *J}](http://www.alciro.org/cgi/tex.cgi?T(f)\ =\ T_L(f)+\left( J*\frac{2*\pi }{n*p}\right)*\frac{\partial f}{\partial t}\\ \frac{\partial f}{\partial t}\ =\ \left[ T(f)-T_L(f) \right]*\frac{n*p}{2*\pi *J}) (5.17)
(5.17)
Cette équation peut être intégrée à trouver le temps t nécessaire pour atteindre le ratio d'étapes f, lorsque le moteur accélère.
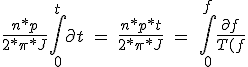-TL(f)}) (5.18)
(5.18)
En général, cette intégrale peut être mis en œuvre graphique, comme les fonctions T (f) et T L (f) ne sont pas des fonctions analytiques. Figure 5.7 (b) montre la fonction 1 / [T (f)-T L (f)] dans la zone ombrée A 1, correspondant à l'intégrale de cette fonction par rapport au ratio de mesures entre 0 et f 1. Le 1 fois t pour le rapport d'étapes f 1 peut être obtenu à partir de l'équation 5.18:
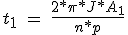 (5.19)
(5.19)
Le profil de vitesse complète pour l'accélération peut être obtenue en répétant ce processus pour une série d'étapes donné raison à atteindre le ratio de gigogne f m. Le processus peut être simplifié si T (f) et M T (f) peut être assimilée à une fonction analytique, comme l'exemple suivant.







