5.1.4.1. Velocity profile equations
\ =\ T_L(f)+J*\left( \frac{\partial^2 \theta }{\partial t^2} \right)) (5.15)
(5.15)
For an n-phase motor with the rotor teeth and p the length of steps is 2 * π / n * p, and the ratio of steps is related to the speed of the rotor:
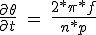 (5.16)
(5.16)
substituting equation 5.15 in the 5.15
![Substituting equations T(f)\ =\ T_L(f)+\left( J*\frac{2*\pi }{n*p}\right)*\frac{\partial f}{\partial t}\\ \frac{\partial f}{\partial t}\ =\ \left[ T(f)-T_L(f) \right]*\frac{n*p}{2*\pi *J}](http://www.alciro.org/cgi/tex.cgi?T(f)\ =\ T_L(f)+\left( J*\frac{2*\pi }{n*p}\right)*\frac{\partial f}{\partial t}\\ \frac{\partial f}{\partial t}\ =\ \left[ T(f)-T_L(f) \right]*\frac{n*p}{2*\pi *J}) (5.17)
(5.17)
This equation can be integrated to find the time t needed to reach the ratio of f steps, when the engine accelerates.
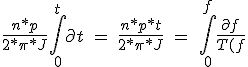-TL(f)}) (5.18)
(5.18)
In general this integral can be implemented graphically, as the functions T (f) and T L (f) are not analytical functions. Figure 5.7 (b) shows the function 1 / [T (f)-T L (f)] in the shaded area A 1, corresponding to the integral of this function with respect to the ratio of steps between 0 and f 1. The time t 1 for the ratio of steps f 1 can be obtained from equation 5.18:
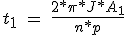 (5.19)
(5.19)
The full velocity profile for acceleration can be obtained by repeating this process for a range of reason given steps to reach the ratio of pull-out f m. The process can be simplified if T (f) and T M (f) can be approximated to an analytic function, such as the following example.







