2.2.5.2. 动态扭矩计算(拔)
现在,我们需要建立之间的电压和电流的基本组成部分,与对相位的关系。在每个阶段的机械动力输出是简单的电流通过感应电压的相位和产品。
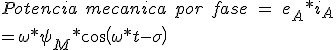*I.cos(\omega *t-\sigma -a)\\ =\frac{\omega *\psi _M*I*cos(a)}{2}+\frac{\omega *\psi _M*I*cos(2*\omega *t-2*\sigma -a)}{2}) (3.25)
(3.25)
从式3.25随时间变化的组件没有兴趣,只需要评估的第一项。对于两相混合,总机械功率为:
) (3.26)
(3.26)
的(a)项人名消除该行与机管局在向量图(图3.24)的建设在一到载体苏黎世角从这个方程。

图3.23。施工图的表达载体本人*职业导向(一)。
该米表达式ωδ线的长度机管局是投影向量,V和苏黎世就行了:
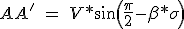\ =\ \omega *\psi _M*cos(\beta )+Z*I*cos(\alpha ))
然后。
\ =\ \frac{V*sin(\frac{\pi }{2}-\beta +\sigma)-\omega *\psi _M*cos(\beta ) }{Z}\\ =\ \frac{V*cos(\beta -\sigma)-\omega *\psi _M*cos(\beta ) }{Z}) (3.27)
(3.27)
代我在方程3.26 3.27 *余弦公式(α)。
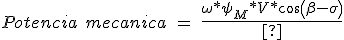-\omega ^2*{\psi _M}^2*cos(\beta ) }{Z}) (3.28)
(3.28)
但是机械功率输出等同于对产品的速度。从方程3.18的速度是ω/ d和这样的:
![转矩方程的混合式步进电机 Par\ =\ \frac{Potencia}{Velocidad}\ =\ \frac{d*[\psi _M*V*cos(\beta -\sigma)-\omega *{\psi _M}^2*cos(\beta )] }{Z}](http://www.alciro.org/cgi/tex.cgi?Par\ =\ \frac{Potencia}{Velocidad}\ =\ \frac{d*[\psi _M*V*cos(\beta -\sigma)-\omega *{\psi _M}^2*cos(\beta )] }{Z}) (3.29)
(3.29)
找到固定的速度在3.29唯一的变量方程的参数是负载角(σ)。这种变化与负载保持一致,电机和负载转矩是平等的。当应用负载,负载角类似的扭矩表现。分析方程3.29发生的最大扭矩当β=σ,则:
![方程牵出转矩步进电机 Par_{(Pull\ out)}\ =\ \frac{d*[\psi _M*V-\omega *{\psi _M}^2*cos(\beta )] }{Z}\\ =\frac{d*\psi _M*V}{\left( R^2+\omega ^2*L^2 \right)^{1/2}}-\frac{d*\omega * {\psi _M}^2*R}{\left( R^2+\omega ^2*L^2 \right)}](http://www.alciro.org/cgi/tex.cgi?Par_{(Pull\ out)}\ =\ \frac{d*[\psi _M*V-\omega *{\psi _M}^2*cos(\beta )] }{Z}\\ =\frac{d*\psi _M*V}{\left( R^2+\omega ^2*L^2 \right)^{1/2}}-\frac{d*\omega * {\psi _M}^2*R}{\left( R^2+\omega ^2*L^2 \right)}) (3.30)
(3.30)
低速扭矩曲线相当于拉出(δψ 米五)/河这两人也可以推导出静态转矩特性,使用3.2.2描述的方法,磁通量(ψm)可以表示基于静态扭矩峰值的条款。
当增加比例的步骤,动态扭矩(拉出)是逐步降至零的水平在一定的速度ω 米 (图3.25)。
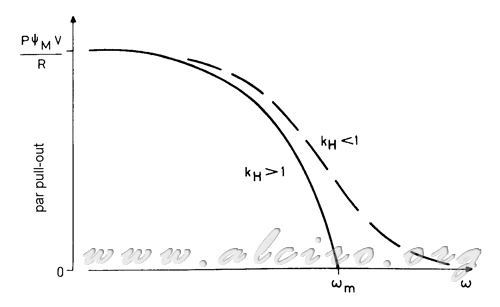
图3.25。波形扭矩/转速扭矩取得了计算上拉了混合式步进电机。
对于另一个响应,物业渐近的轴T = 0时,两人是在一零相切无限步骤的比例。
等同于零方程3.30一对夫妇得到最大的速度ωm:
^{1/2}}-\frac{d*\omega * {\psi _M}^2*R}{\left( R^2+\omega ^2*L^2 \right)}\ =\ 0)
因此;
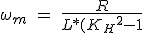^{1/2}}) (3.31)
(3.31)
可移动机器人因次周波数kh = / VL的电机常数。对于方程3.31的最大工作频率只能获得如果是大于1因次周波数kh在这种情况下,分母中的平方根可以评估实际价值。的步骤为3.31最大速率方程为:
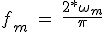 (3.32)
(3.32)
最大工作频率是从3.31方程获得是成正比的阶段(R)的总电阻,因此,如果引擎在高速运行时,电源电路必须包括强大的阻力。
对于发动机的选择要工作在高的速度是可取的的KH值尽可能低,使分母的表达获得最大的频率降至最低。







