2.2.5.1. Modell einer Hybrid-Schrittmotor
Der erste Schritt bei der Berechnung des Paares ist das Modell für einen Motor Phase (Abbildung 3.21) festgelegt. Ein Hybrid-Motor verfügt über zwei unabhängige Wunde Etappen auf dem Stator, das Modell für jede Phase einschließlich der Widerstand und die Induktivität der Spule befestigt. Der Widerstand des Drahtes und die Wicklungsinduktivität Eigenschaften, die wir durch den Hersteller bestimmt sind.
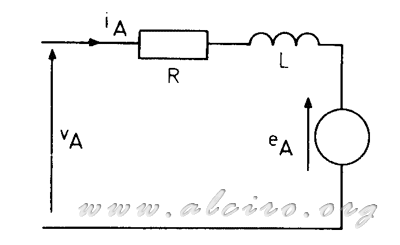
Abbildung 3.21. Model-Schaltung für eine Phase eines Hybrid-Motors.
Zur Vervollständigung des Modells muss die induzierte Spannung in der Wicklung der Phase durch die Einwirkung des Rotors sind. Diese Spannung wird durch die Strömung durch den Permanentmagneten erzeugt verursacht, variierende sinusförmige mit Bezug auf die Position des Rotors. Die Strömung in der Phasen A und B mit einem Motor mit dem Rotor Zähne d ausgedrückt werden als induziert:
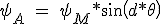\\ \psi _B\ =\ \psi _M*sin(d*\theta-\frac{\pi }{2} )) (3.15)
(3.15)
ψm den maximalen Durchfluss in jeder Wicklung induziert. Wenn der Rotor bewegt sich mit dq / dt, die induzierte Spannung in der Wicklung der Phase gleichwertig ist zu fließen Änderungen induziert.
*\frac{\partial \theta }{\partial t}\\ e_A\ =\ \frac{\partial \psi _B}{\partial t}\ =\ d*\psi _M*cos(d*\theta -\frac{\pi }{2})*\frac{\partial \theta }{\partial t}) (3.16)
(3.16)
Die induzierte Spannung Merkmale sind in der Regel nicht in den Daten vom Hersteller geliefert inbegriffen, kann aber experimentell gewonnen werden. Wenn die Motorwicklungen Leerlauf gelassen werden, und die Welle ist es zu einem anderen Motor in Bewegung angeschlossen, wird die Spannung in der Phase gemessen in Höhe der induzierten Spannung. Die Kenntnis der Geschwindigkeit (dq / dt) Leerlaufspannung (e) und die Anzahl der Rotorzähne (d), Peak-Flow (ψ m) 3,16 bestimmt werden unter Verwendung von Gleichung. Eine weitere Alternative ist die Geschwindigkeit schließen ψ m der Merkmale der Drehmoment /, arbeiten bei niedrigen Drehzahlen.
Die Hybrid-Schrittmotoren haben zwei Phasen, die mit positiven oder negativen Strom angeregt werden kann. Eine vollständige Zyklus der Anregung bietet vier Stufen, entsprechend der Anregung der einzelnen Phase mit dem Strom in beiden Polaritäten. Wenn der Motor bei einer Geschwindigkeit von f Schritten wird der Zyklus Erregerfrequenz f / 4 und die Winkelgeschwindigkeit für einen Zyklus von Erregung wiederholt wird:
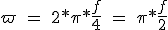 (3.17)
(3.17)
Während jedes Zyklus der Anregung der Motor zieht ein Feld Zahn (Zahnteilung = 2π / d) in einer Zeit, 2π / ω, und die durchschnittliche Geschwindigkeit des Rotors ist:
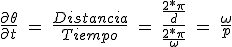 (3.18)
(3.18)
Integration dieser Gleichung über die Zeit.
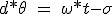 (3.19)
(3.19)
Σ eine Konstante der Integration als Lastwinkel bekannt. Dieser Winkel ist durch die Verzögerung bei der Position des Rotors in Bezug auf die Gleichgewichtslage der Bühne gebildet, mit steigender Belastung (siehe Ziffer 3.2.2).
Die Spannung an jeder Phase von einer Phase der kontinuierlichen Strom gewonnen und kann in eine positive oder negative geschaltet werden. Dieser Schaltvorgang führt eine Nichtlinearität, die entfernt werden können, ausschließlich für die grundlegende Komponente der Spannung und Strom. Das Drehmoment des Motors ist abhängig von der Interaktion von Intensität und Phase induzierten Spannung. Die induzierte Spannung ist im wesentlichen sinusförmige und nur die sinusförmige Komponente des Stroms durch die Phase mit der gleichen Frequenz ist für die Berechnung des Paares erforderlich.
Setzt man Gleichungen 3.18 und 3.19 in 3.16 finden wir die Expression von Stress.
) (3.20)
(3.20)
Die Frequenz der induzierten Spannung ist gleich der Frequenz der Grundschwingung der Spannung, und nur die grundlegende Komponente der Strom wird für die Berechnung des Paares notwendig.
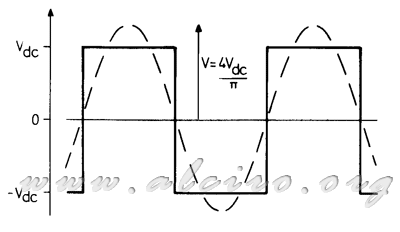
Abbildung 3.22. Waveform Spannung in einer Phase eines hybriden Anregung Sequenz, die mit zwei aktiven Phasen, welche die Spannung grundlegende Komponente.
Die grundlegende Komponente der Versorgungsspannung hat eine Amplitude von V = 4V dc / π, wo Vdc ist die DC-Spannungsversorgung. Die grundlegende Komponente der Phasenspannung kann geschrieben werden als:
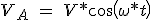\\ V_B\ =\ V*cos(\omega *t-\frac{2}{\pi })) (3.21)
(3.21)
momentane Spannung und Strom für Phase A ist durch die Gleichung ausgedrückt.
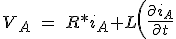+e_A) (3.22)
(3.22)
Die grundlegende Komponente der Strom durch die Phase A kann wie folgt ausgedrückt werden:
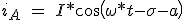) (3.23)
(3.23)
wobei a der Phasenwinkel. Setzt man die fundamentale Spannung und Strom-Komponente in der Gleichung 3,22 ergibt sich:
\ =\ R*I*cos(\omega *t-\sigma -a)-\omega *L*I*sin(\omega *t-\sigma -a)+\omega *\psi _M*cos(\omega *t-\sigma )) (3.24)
(3.24)
Das Zeigerdiagramm für diese Gleichung kann in Abbildung 3.23 zu sehen.

Abbildung 3.23. Schematische Darstellung der Vektoren mit den Komponenten einer Phase für einen Hybrid-Motor.
Im Zeigerdiagramm der Spannung, die Phase ist gleich der Summe Wert der induzierten Spannung und Dehnung auf den Widerstand und die Induktivität. Die Spannung am Widerstand ist in Phase mit dem Strom, während die Spannung in der Spule wird der Strom in π / 2 versetzt. Die induzierte Spannung führt die aktuelle von der Bühne in einem Winkel zu und ist auf die Spannung in einem Winkel δ angewandt verzögert. In diesem Zeigerdiagramm berücksichtigt nur die grundlegenden Strom, obwohl dies durch eine Reihe von höheren Harmonischen Frequenz ausgebildet ist, sie nicht auf das Drehmoment vom Motor erzeugte beitragen.







